Day 4 - Entropy, Statistics, and Wordle?

05 Jan 2025

Building a Wordle Analysis Tool

Introduction

Yesterday, we explored using Python and Streamlit to create a simple web application. Today, we’re taking it further by combining web development with data science principles to solve a fun and popular challenge: Wordle!

Wordle is an excellent playground for applying basic statistics and data science. It’s simple, relatable, and offers plenty of opportunities to explore probability, entropy, and decision-making. To make things even better, I’ve built and deployed a Wordle Solver app using Python and Streamlit. You can try it out here, or explore the code on GitHub.

---

Part 1: Why Wordle Makes for a Great Data Science Playground

1. Popularity and Familiarity
   Wordle is a household name, with its straightforward rules and universal appeal. This makes it an ideal starting point for demonstrating data-driven decision-making.

2. Data/Stats in Action
   Each guess in Wordle provides valuable feedback, narrowing the list of possible solutions. By analyzing this feedback, we can make smarter guesses.

3. Simple, Yet Complex
   Wordle combines simplicity with strategic depth, making it a fantastic problem for exploring probability, statistics, and entropy.

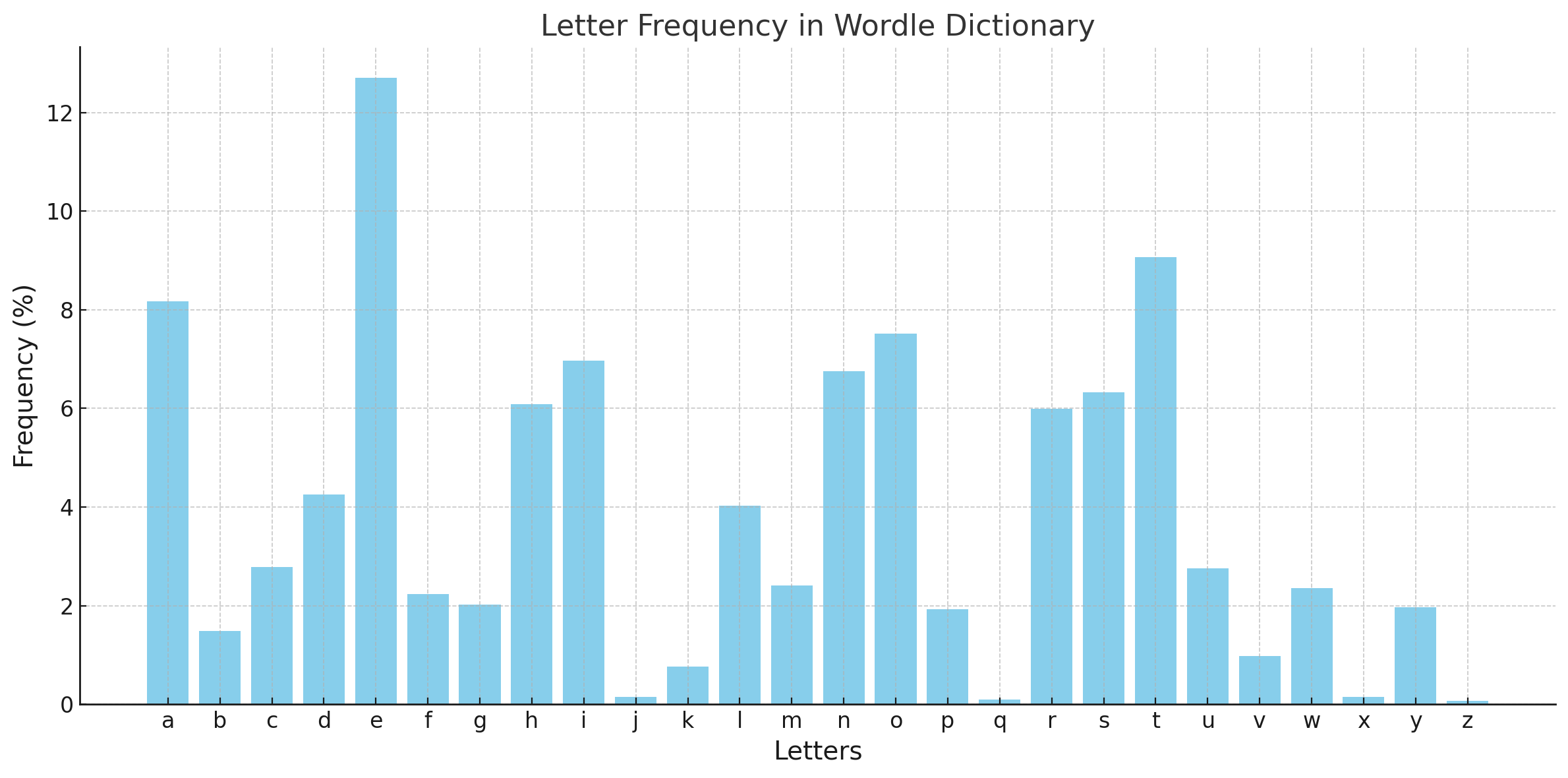
Visualization: Here’s a chart showing the frequency of letters in the Wordle dictionary. Notice how vowels like E dominate while less common letters like Z barely register.

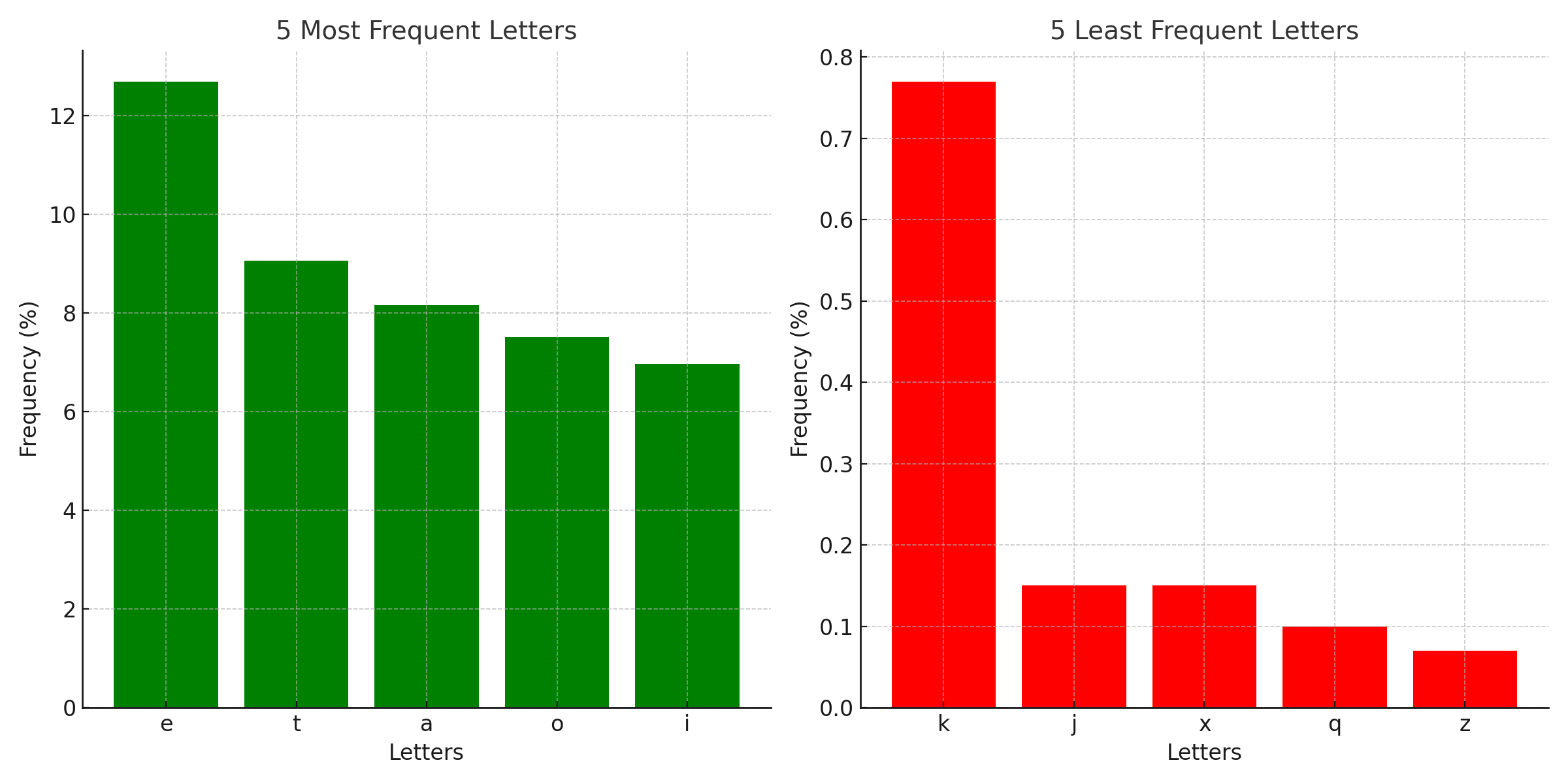
Most and Least Frequent Letters: Below are the 5 most and 5 least frequent letters in Wordle.

Why Letter Frequency Analysis Matters

In Wordle, the first guess is critical—it sets the stage for everything that follows. A good first guess uses common letters, increasing the likelihood of a match.

For example:

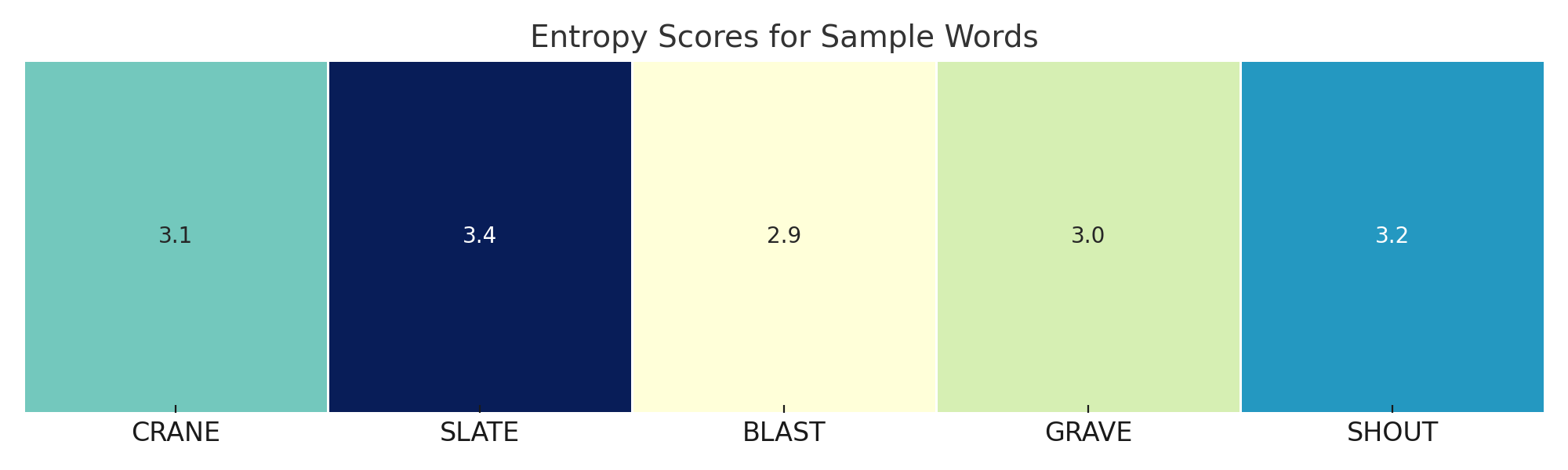
• Words like CRANE or SLATE maximize the use of frequent letters (E, A, T).
• Conversely, words with rare letters, like QUIZ or JUMPY, are less effective at the start.

---

Part 2: What is Entropy (and Why Does It Matter)?

Entropy in Information Theory

Entropy is a measure of uncertainty. In Wordle, entropy helps us determine which guess provides the most “information gain.” A good guess splits the remaining word list into evenly distributed subsets based on possible feedback patterns.

Why High Entropy is Better

A high-entropy guess:

• Reduces the solution space more effectively.
• Ensures you don’t leave too many possibilities after one guess.

Example:

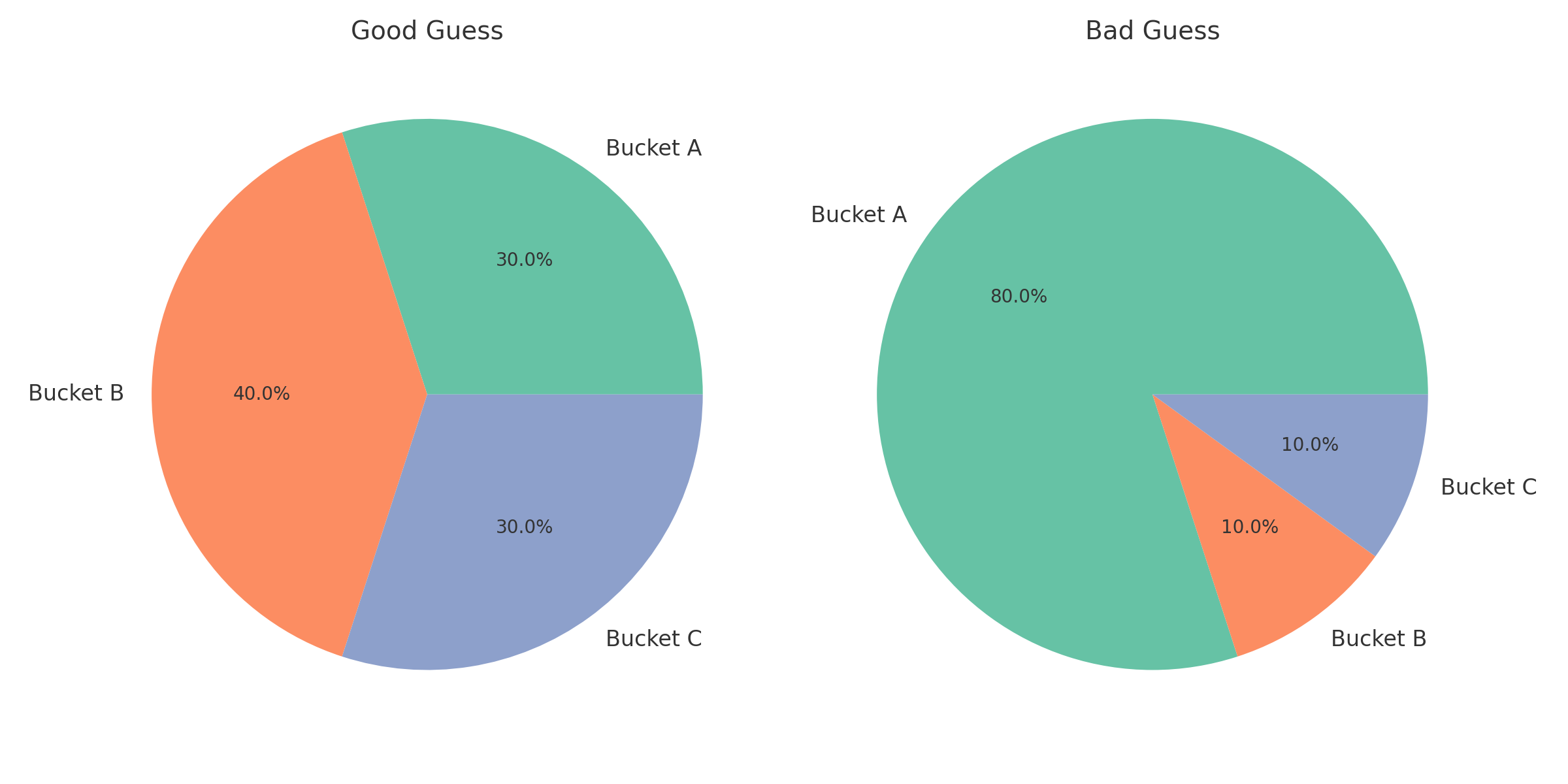
• A good guess splits 100 possible solutions into groups of 25, 25, 25, and 25 (high entropy).
• A bad guess leaves one group with 90 solutions and another with 10 (low entropy).

Visualization: Good vs. Bad Guesses

Below are examples of how good and bad guesses partition the solution space:

Part 3: Step-by-Step Instructions to Build the Wordle Solver App

Prerequisites:

1. Install Python (3.7 or later).
2. Install Streamlit:

   pip install streamlit
   

3. Download the word lists: words_alpha.txt and words_enable.txt from GitHib (https://github.com/j-abed/wordle-solver)

---

Step 1: Create the MVP (Minimal Viable Product)

File: wordle_solver.py

1. Set up the environment: Create a new Python file wordle_solver.py.
2. Load the Wordle word list:

   def load_words(file_path):
       with open(file_path, 'r') as file:
           return [line.strip() for line in file if len(line.strip()) == 5]
   word_list = load_words('words_alpha.txt')
   

3. Filter words based on feedback:

   def filter_words(word_list, guess, feedback):
       filtered = []
       for word in word_list:
           valid = True
           for i, (g, f) in enumerate(zip(guess, feedback)):
               if f == 'g' and word[i] != g:  # Green
                   valid = False
               elif f == 'y' and (g not in word or word[i] == g):  # Yellow
                   valid = False
               elif f == 'b' and g in word:  # Black
                   valid = False
           if valid:
               filtered.append(word)
       return filtered
   

4. Add Streamlit UI:

   import streamlit as st
   
   st.title("Wordle Solver (MVP)")
   
   guess = st.text_input("Enter your guess:")
   feedback = st.text_input("Enter feedback (e.g., G for green, Y for yellow, _ for gray):")
   
   if st.button("Filter Words"):
       filtered_words = filter_words(word_list, guess, feedback)
       st.write("Remaining possible words:", filtered_words)
   

5. Run the MVP app:

   streamlit run wordle_solver.py
   

---

Step 2: Add Entropy-Based Enhancement

File: enhanced_wordle_solver.py

1. Simulate feedback for all guesses:

   def evaluate_guess(solution, guess):
       feedback = ['b'] * 5  # Default to black (incorrect)
       solution_chars = list(solution)
   
       # Green matches
       for i, (s, g) in enumerate(zip(solution, guess)):
           if s == g:
               feedback[i] = 'g'
               solution_chars[i] = None
   
       # Yellow matches
       for i, g in enumerate(guess):
           if feedback[i] == 'b' and g in solution_chars:
               feedback[i] = 'y'
               solution_chars[solution_chars.index(g)] = None
   
       return ''.join(feedback)
   

2. Calculate entropy for each word:

   import math
   
   def calculate_entropy(guess, possible_words):
       feedback_buckets = {}
       for word in possible_words:
           feedback = evaluate_guess(guess, word)
           feedback_buckets[feedback] = feedback_buckets.get(feedback, 0) + 1
   
       total = sum(feedback_buckets.values())
       entropy = -sum(
           (count / total) * math.log2(count / total)
           for count in feedback_buckets.values()
       )
       return entropy
   

3. Enhance the Streamlit UI:

   if st.button("Get Best Guess"):
       entropy_scores = {word: calculate_entropy(word, word_list) for word in word_list}
       best_guess = max(entropy_scores, key=entropy_scores.get)
       st.write("Best next guess:", best_guess)
   

---

Part 4: Experiment with the Colab Notebook

Want to try your own experiments with Wordle strategies? I’ve created a Colab Notebook where you can:

• Load the Wordle word list.
• Simulate guesses and calculate entropy.
• Explore which guesses work best for narrowing down possibilities.

---

Part 5: Conclusion

With this app, you’ve built a fully functional Wordle solver that combines Python, Streamlit, and basic data science principles. Whether you’re playing Wordle or exploring applied statistics, this project demonstrates the power of data-driven decision-making.

Next Steps: How can these concepts extend to other games or real-world problems? Stay tuned for Day 5!

---

• Next: Day 5